Espacio Euclídeo

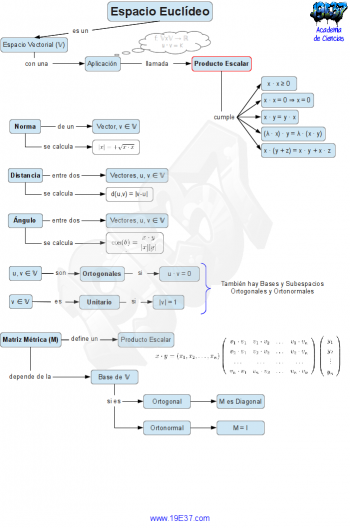
Un Espacio Euclídeo es una estructura algebraica formada por un Espacio Vectorial (𝕍) y una aplicación (·) llamada Producto Escalar.

Mapa Conceptual

Producto Escalar

El Producto Escalar es una aplicación entre dos vectores que tiene como resultado un escalar. Puede expresarse como: \[ \begin{array}{rrcl} \langle \cdot,\cdot \rangle : & \; V \times V & \longrightarrow & \mathbb{K} \\ & (x,y) & \longrightarrow & a = \langle x, y \rangle \end{array} \]

Propiedades del Producto Escalar

Para que una aplicación sea producto escalar debe cumplir las siguientes propiedades:

• Definida Positiva: \(∀ \vec x ∈ \mathbb{V};~ \vec x · \vec x \ge 0\). Y \(\vec x · \vec x = 0 \Leftrightarrow \vec x = 0\)
• Conmutativa: \(∀ \vec x, \vec y ∈ \mathbb{V};~ \vec x · \vec y = \vec y · \vec x\)
• Asociativa: \(∀ \vec x, \vec y ∈ \mathbb{V}, \lambda ∈ \mathbb{R};~ (\lambda · \vec x) · \vec y = \lambda · (\vec x) · \vec y\)
• Distributiva: \(∀ \vec x, \vec y ∈ \mathbb{V}, \lambda ∈ \mathbb{R};~ \lambda · (\vec x + \vec y) = \lambda · \vec x + \lambda · \vec y\)

Norma de un Vector

La existencia de producto escalar nos permite definir la Norma de un Vector como\[|\vec x| = +\sqrt{\vec x · \vec x}\]

Y nos permite definir también los siguientes conceptos:

Distancia entre dos Vectores

La distancia entre dos vectores se define como\[d(\vec x, \vec y) = |\vec y - \vec x|\]

Ángulo entre dos Vectores

El ángulo entre dos vectores se define como\[\widehat{\vec x, \vec y} = \theta \rightarrow cos(\theta) = \frac{\vec x · \vec y}{|\vec x| · |\vec y|}\]

Ortogonalidad

Dos vectores son ortogonales si su ángulo es π/2. Lo cual equivale a\[\vec x · \vec y = 0\]

Vector Unitario

Llamamos vector unitario al que tiene norma 1\[|\vec u| = 1\]

Bases y Subespacios Ortogonales y Ortonormales

Extendiendo estos conceptos, es posible definir bases y subespacios ortogonales y ortonormales:

• Una Base es Ortogonal si está formada por vectores ortogonales entre sí.
• Una Base es Ortonormal si está formada por vectores unitarios ortogonales entre sí.
• Dos Subespacios son Ortogonales si todos los vectores del primero son ortogonales a todos los vectores del segundo.
• El Subespacio Ortogonal a un vector está formado por todos los vectores ortogonales al dado.

Matriz Métrica

Todo producto escalar puede definirse mediante una Matriz Métrica, tal que\[\vec x · \vec y = X·M·Y = \left(\begin{matrix}x_1 & x_2 & \cdots & x_n\end{matrix}\right) · \left(\begin{matrix} \vec v_1 · \vec v_1 & \vec v_1 · \vec v_2 & \cdots & \vec v_1 · \vec v_n \\ \vec v_2 · \vec v_1 & \vec v_2 · \vec v_2 & \cdots & \vec v_2 · \vec v_n \\ \vdots & \vdots & \cdots & \vdots \\ \vec v_n · \vec v_1 & \vec v_n · \vec v_2 & \cdots & \vec v_n · \vec v_n \end{matrix}\right) · \left(\begin{matrix}y_1 \\ y_2 \\ \vdots \\ y_n\end{matrix}\right) \]

Donde las matrices X e Y son las matrices de coordenadas de los vectores en la base del subespacio \(B=\{\vec v_1, \vec v_2, \cdots, \vec v_n\}\) y M es la matriz métrica.

Puede observarse que, si la base B es ortogonal, la matriz M será diagonal. Y que si la base B es ortonormal, la matriz M será la matriz identidad.

Podemos utilizar la matriz métrica para comprobar que en todo producto escalar, los menores principales de la matriz métrica son todos positivos.